Everything You Need to Know About Variables and Expressions
Table of Contents
Nosotros at Cuemath believe that Math is a life skill. Our Math Experts focus on the "Why" behind the "What." Students can explore from a huge range of interactive worksheets, visuals, simulations, practice tests, and more than to empathize a concept in depth.
Book a FREE trial class today! and experience Cuemath's Alive Online Grade with your kid.
Introduction to Variable Expressions
James and Natalie were playing with match sticks and they idea of forming patterns of numbers using the matchsticks.
James took 4 match sticks and formed the number \(4\)

Natalie added 3 more lucifer sticks to form a pattern with two \(iv\)s.

Then James again added 3 more friction match sticks to course a pattern with iii \(4\)s.

All of a sudden, Natalie got a doubt that how many match sticks are required to make a pattern of ten \(4\)s?
They understood from the existing pattern that they demand \(4+ 9 (3)\) sticks to get it done as they want a pattern with ten \(4\)south.
From this, they concluded that they need \(4+(n-1)3\) sticks, in general, to make a pattern with \(n\) number of \(four\)s.
Here, \(4+(n-1)3\) is called an algebraic expression.
Definition of Variable, Abiding, Term and Coefficient
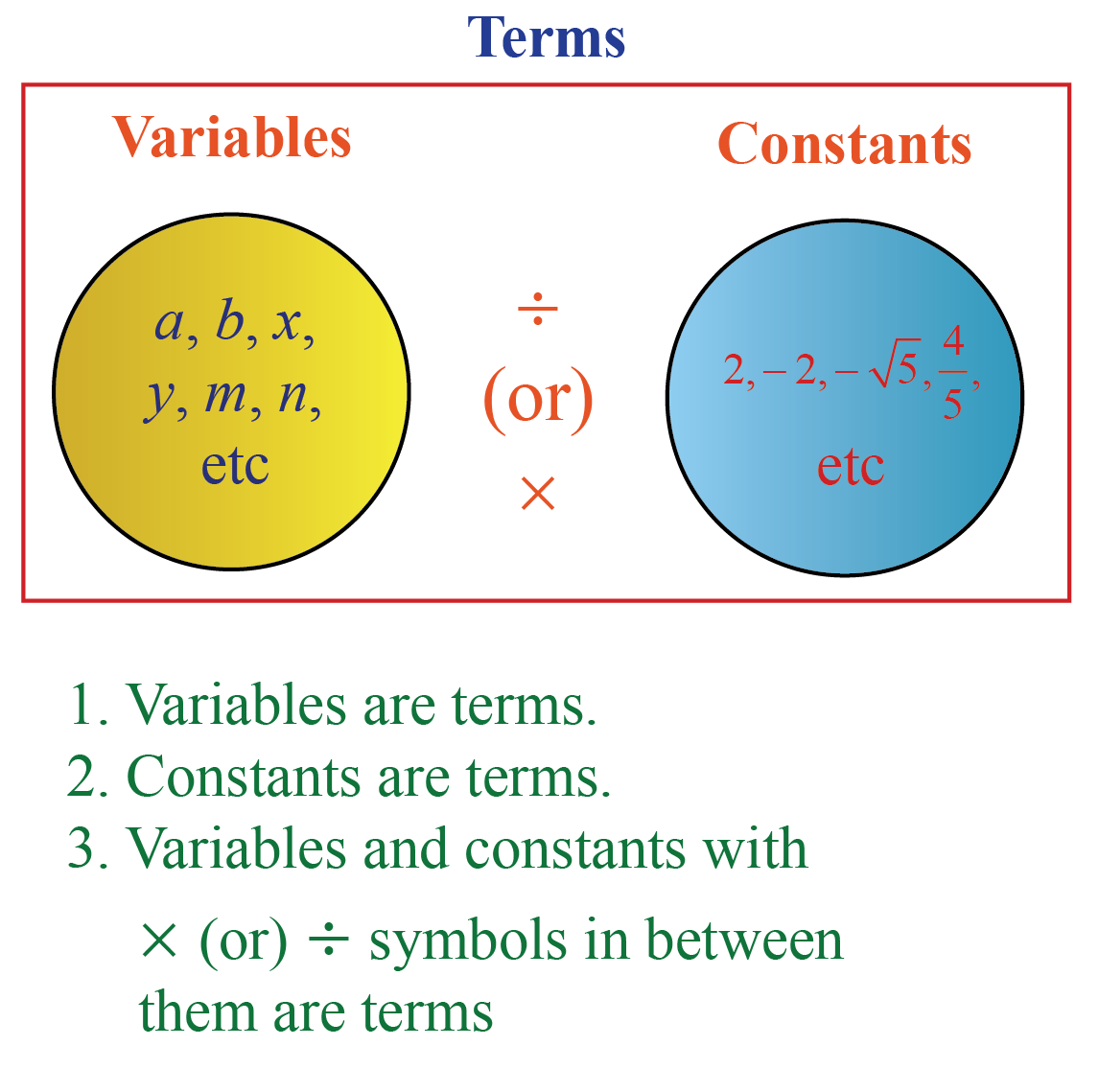
- A symbol that doesn't take a fixed value is chosen a variable in Math. It can have any value.
In the above example, \(n\) is a variable and hither it tin can take the values \(ane,2,iii,...\)
Some examples of variables in Math are \(a,b, 10, y, z, m, \) etc.
- A symbol that has a stock-still numerical value is called a constant.
All numbers are constants.
Some examples of constants are \(3, 6, \dfrac{-1}{2}, \sqrt{5}\) etc.
- A term is a variable lonely (or) a constant solitary (or) information technology tin be a combination of variables and constants by the performance of multiplication or division.
Some examples of terms are \(3x^ii, \dfrac{-2}{3}y, \sqrt{5m},\) etc.
Here, the numbers that are multiplying the variables are \(3, \dfrac{-2}{3} \) and \(5\) which are called coefficients.
CLUE less in Math? Check out how CUE MATH Teachers will explain Variable Expressions to your kid using interactive simulations & worksheets and so they never have to memorise anything in Math again!
Explore Cuemath Live, Interactive & Personalised Online Classes to make your kid a Math Expert. Book a FREE trial class today!
Variable Expression (Algebraic Expression)
A variable expression (or) an algebraic expression is a combination of terms by the operations such as addition, subtraction, multiplication, segmentation, etc.
Case of a Variable Expression
An example of a variable expression (or) an algebraic expression is \(5x + 7\)

Evaluating a Variable Expression
To evaluate a variable expression at a given value, we just substitute that value in the expression and simplify it.
Examples:
Evaluate \(5x^2+2x+7\) at \(ten= -2\)
Solution:
Substitute \(x=-2\) in \(5x^ii+2x+vii\),
\[\begin{align}5(-2)^2+2(-two)+7 &= 5(4)-4+vii \\&= twenty-iv+vii\\&= 23\end{align}\]
Then the answer is \(23\)
Types of Variable Expressions
There are \(v\) types of variable expressions (or) algebraic expressions.
| Types | Significant | Examples |
|---|---|---|
| Monomial | An expression with but i term where the exponents of all the variables are non-negative integers | \(3xy\) |
| Binomial | An expression with two monomials | \(\dfrac{3}{4}ten - 2y^2\) |
| Trinomial | An expression with 3 monomials | \( 3x-2y+ z\) |
| Polynomial | An expression with ane or more monomials | \(\dfrac{-ii}{3}ten^three\!\!+\!7x^2\!+\!3x\!+\!v\) |
| Multinomial | An expression with one or more than terms (the exponents of variables can be either positive or negative) | \(4x^{-1} +2y+3z\) |

Think Tank
- Is every polynomial a multinomial?
- Is every multinomial a polynomial?
Activity on Evaluating the Variable Expressions
Hither is an action on Variable Expressions.
From this, yous tin select one of the given variable expressions and requite the value(south) for its variable(s).
Then you tin can evaluate and enter the value of the variable expression's solution as per the values you gave.
Don't worry if you enter an wrong respond for the expression.
It will prove you a step-past-step explanation of the correct answer.
Aid your kid score college with Cuemath'south proprietary Gratuitous Diagnostic Test. Get access to detailed reports, customized learning plans, and a Free counseling session. Attempt the test now.
Solved Examples
There are \(25\) oranges in a purse. Write the variable expression (algebraic expression) for the number of oranges in \(x\) number of bags.
Solution:
The number of oranges in one bag = \(25\)
The number of numberless = \(ten\)
So the number of oranges in \(x\) bags = \(25x\)
Required Variable Expression \(= 25x \)
Evaluate the given variable expression for \(a = vii; b = -three\) and \(c = ii\)
\[6ab + 7bc + 9ca\]
Solution:
The given algebraic expression is \(6ab + 7bc + 9ca\)
Substitute the beneath values in the in a higher place expression:
\(a = 7; \;b = -3; \; c = 2\)
\[\begin{align}6ab \!+\! 7bc \!+\! 9ca&\!=\! 6(7)(-3) \!+\! 7(-3)(ii) \!+\! 9(ii)(7)\\[0.3cm]&\!=\!\!-\!126\!-\!42\!+\!126\\[0.3cm]&\!=\!\!-\!42\end{align}\]
\[6ab + 7bc + 9ca = - 42 \]
Identify the correct option (s).
\(4x+five\) is a ...
(a) Monomial
(b) Binomial
(c) Trinomial
(d) Polynomial
Solution:
\(4x+two\) has two monomials \(4x\) and \(5\) and hence it is a binomial.
Every binomial is a polynomial also. So \(4x+five\) is a polynomial besides.
So the correct answers are:

Challenging Questions
- How many terms are there in the algebraic expression \(4x^2y^ii + \dfrac{3}{x}-y\)?
- What is an algebraic expression with \(iv\) monomials called?
- What is the algebraic expression for the statement "3 more than 5 times the sum of \(10\) and \(y\)"?
- Evaluate the algebraic expression \(x^2-3x+2\) at \(x=ii\)
Practise Questions
Important Topics
Given beneath are the list of topics that are closely connected to variable expressions. These topics will too give you a glimpse of how such concepts are covered in Cuemath.
- Add-on and Subtraction
- Factorization
Maths Olympiad Sample Papers
IMO (International Maths Olympiad) is a competitive exam in Mathematics conducted annually for school students. Information technology encourages children to develop their math solving skills from a competition perspective.
You tin can download the Costless class-wise sample papers from below:
- IMO Sample Paper Class 1
- IMO Sample Paper Class 2
- IMO Sample Paper Course 3
- IMO Sample Paper Class iv
- IMO Sample Paper Class 5
- IMO Sample Paper Class 6
- IMO Sample Newspaper Course 7
- IMO Sample Newspaper Class viii
- IMO Sample Paper Class nine
- IMO Sample Newspaper Class 10
To know more about the Maths Olympiad you tin can click hither
Frequently Asked Questions (FAQs)
1. How do you write a variable expression?
A variable expression depends on the condition.
For exam, "\(3\) more than \(10\)" tin can be written as the variable expression \(x+3\)
"\(7\) less than the sum of \(a\) and \(b\)" tin exist written equally the variable expression \(a+b-7\)
2. What is a variable instance?
A symbol that doesn't have a fixed value is called a variable in Math. It tin take any value.
Some examples of variables in Math are \(a,b, x, y, z, m, \) etc.
You can find more than information under "Definition of Variable, Abiding, Term and Coefficient" section of this page.
three. What are the 3 types of variables?
The 3 types of variables are:
- Independent variables
- Dependent variables
- Controlled variables
four. Practise expressions always demand to have a variable?
No, an expression doesn't necessarily need to have a variable.
For example, the constants like \(2, -3, \dfrac{-3}{4}\) are also called equally expressions.
v. How do you define a variable?
A symbol that doesn't have a fixed value is chosen a variable in Math. It can accept whatever value.
Some examples of variables in Math are \(a,b, 10, y, z, m, \) etc.
half-dozen. What is a variable? Give an case.
A symbol that doesn't accept a fixed value is called a variable in Math. It tin take any value.
Some examples of variables in Math are \(a,b, x, y, z, m, \) etc.
Source: https://www.cuemath.com/algebra/variable-expressions/
Post a Comment for "Everything You Need to Know About Variables and Expressions"